Secant method

Numerical methods

Root bracketing methods

• Bisection method
• Regula Falsi
• Brent method

Root polishing methods

• Newton method
• Secant method

Secant method is a simplified version of Newton method that does not require the computation of the derivative.

The secant method is defined by the recurrence relation:

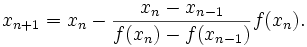
As can be seen from the recurrence relation, the secant method requires two initial values, x₀ and x₁, which should ideally be chosen to lie close to the root. Iterations avoid the evaluation of the derivative by replacing it with a numerical estimate, the slope through the previous two points.

When the derivative does not change significantly near the root, secant method gives a useful saving. On single roots, the method has a convergence of order approximately 1.618 (the golden ratio). Secant converges linearly for multiple roots. Since the secant method does not always bracket the root, the algorithm may not converge for functions that are not sufficiently smooth.

PROCEDURE Secant(a, b, eps:Real; VAR xsol:Real);

VAR

   c, fb:Real;

BEGIN

{ df(x) = value of the first derivative }

{ eps = accuracy of the root, e.g.: 0.000001 }

   REPEAT

     fb=f(b);

     c:=a-(b-a)*fb/(fb-f(a))

     a:=b;

     b:=c;

   UNTIL Abs(a-b)<eps;

   xsol:=c

END; {Secant method - Pascal code}

Muller's method is a numerical analysis method for root finding, based on secant method. It is first presented by D. E. Muller in 1956. Instead of two, Muller's method uses three initial approximations. The intersection of the x-axis with the parabola through the three approximations and corresponding f(x) is the next approximation.

Numerical methods | Bisection method | Regula Falsi method | Brent method | Newton method | Secant method

See how secant method works, solve equations free and take the results with you.