Regula Falsi method

Numerical methods

Root bracketing methods

• Bisection method
• Regula Falsi method
• Brent method

Root polishing methods

• Newton method
• Secant method

Regula Falsi method (false position) is a root-finding method based on linear interpolation. Its convergence is linear, but it is usually faster than bisection. On each iteration a line is drawn between the endpoints (a,f(a)) and (b,f(b)) and the point where this line crosses the x-axis is taken as a "midpoint". The value of the function at this point is calculated and its sign is used to determine which side of the interval does not contain a root. That side is discarded to give a new, smaller interval containing the root. Regula Falsi method can be continued indefinitely until the interval is sufficiently small. The best estimate of the root is taken from the linear interpolation of the interval on the current iteration.

While secant method retains the most recent of the prior estimates, regula falsi keeps that prior estimate for which the function value has opposite sign from the function value at the current best estimate of the root, so that the two points continue to bracket the root.

PROCEDURE RegulaFalsi(a,b,eps:Real; VAR xsol:Real);

{ Required condition: f(a)*f(b)<0 }

{ eps = accuracy of the root, e.g.: 0.000001 }

VAR

   c, fa, fb:Real;

BEGIN

   REPEAT

     fa:=f(a); fb:=f(b);

     c:=b - (b-a)*fb/(fb-fa);

     IF fa*f(c)<0 THEN b:=c

     ELSE a:=c

   UNTIL b-a<eps;

   xsol:=c

END; {Regula Falsi method - Pascal code}

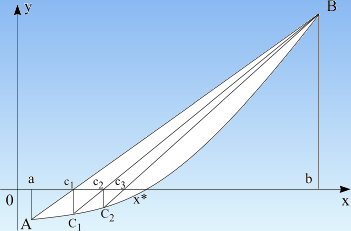
Numerical methods | Bisection method | Regula Falsi method | Brent method | Newton method | Secant method

See how Regula Falsi method works, solve equations free and take the results with you.