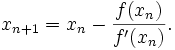
Newton method converges quadratically for single roots, and linearly for multiple roots.
| newton method |
| deadline online |
| download |
| screenshots |
| how to find roots |
| numerical methods |
| Newton C code |
| Newton in-depth |
| plot graphs |
| support center |
Root bracketing methods
Root polishing methods
Newton method is the standard root-polishing algorithm.
Newton method, also called the Newton-Raphson method, is a root-finding algorithm that uses the first few terms of the Taylor series of a function f(x) in the vicinity of a suspected root.
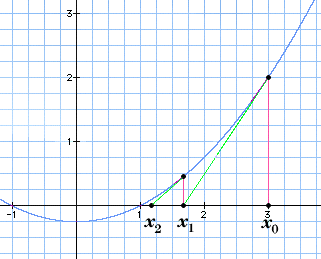
Newton algorithm begins with an initial
guess for the location of the root. On each iteration, a line
tangent to the function f is drawn at that position. The point
where this line crosses the x-axis becomes the new guess.
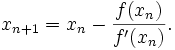
Newton method converges quadratically for single roots, and
linearly for multiple roots.
|
|
The function below, written in Pascal, takes a simpler aproach, ignoring the situation in which Newton method does not converge. For a C implementation of Newton method, grasp Newton.c.
To find more about Newton method, visit the pages below:
Numerical methods | Bisection method | Regula Falsi method | Brent method | Newton method | Secant method
See how Newton method works, solve equations free and take the results with you.