| optimize functions |
| solve equations |
| download |
| screenshots |
| root finding faq |
| numerical methods |
| deadline tutorial |
| parametric equations |
Optimization problem
Find the dimensions of the rectangle of largest area which can be inscribed in the closed region bounded by the x-axis, y-axis, and graph of f(x)=8-x3.
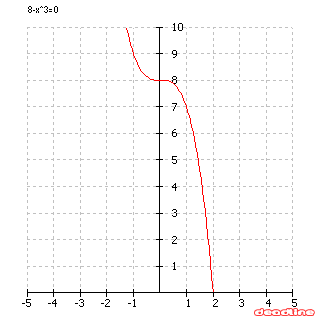
If x is the width of the rectangle, we can conclude that 0<x<=2. Then the height of the rectangle is f(x). So the function that needs to be optimized is g(x)=x*f(x)=x(8-x3).
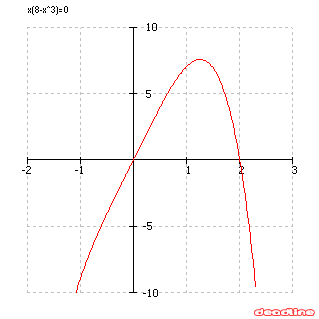
If you use DeadLine to find extrema, you will get x=1.25992105, which is the answer to the problem.
Another optimization problem:
A movie screen on a wall is 20 feet high and 10 feet above the floor. At what distance x from the front of the room should you position yourself so that the viewing angle of the movie screen is as large as possible ? See the solution.
Solve optimization problems, find maximum and minimum of a function using DeadLine.